Napjaink részecskefizikájának legnagyobb
kihívást jelentõ kérdései között
elõkelõ helyet foglalnak el azok, amelyek a szuperszimmetrikus
elméletekkel kapcsolatosak. A következõ oldalakon1
errõl az izgalmas kihívásról ejtünk
szót egy kísérleti fizikus nézõpontjából.
A részecskék
változatos világa
 A
részecskefizika Standard Modellje, amelyrõl bõvebben
Horváth Dezsõcikkében olvashatnak, jól
leírja az anyagi világ alapvetõ szerkezetét
és az anyag kölcsönhatásait. Az elmélet
szerint az anyagrészecskék, a kvarkok és leptonok
három családba rendezõdnek, és köztük
a kölcsönhatásokat a mértékbozonok
közvetítik. Már a Standard Modell elemi részecskéi
- azaz a töltött és semleges leptonok, a kvarkok,
a mértékbozonok és a misztikus Higgs-részecske,
amelyrõl Szillási Zoltánírása
szól - is igen sokfélék. A változatosságot
azonban még tovább növelik azon elméletek,
amelyek az elõttünk álló, a Standard Modell
által meg nem válaszolt és Cynolter Gáborcikkében
már felvázolt kérdéseket egy új
szimmetria, a szuperszimmetriafeltételezésével
kísérlik megválaszolni.
A
részecskefizika Standard Modellje, amelyrõl bõvebben
Horváth Dezsõcikkében olvashatnak, jól
leírja az anyagi világ alapvetõ szerkezetét
és az anyag kölcsönhatásait. Az elmélet
szerint az anyagrészecskék, a kvarkok és leptonok
három családba rendezõdnek, és köztük
a kölcsönhatásokat a mértékbozonok
közvetítik. Már a Standard Modell elemi részecskéi
- azaz a töltött és semleges leptonok, a kvarkok,
a mértékbozonok és a misztikus Higgs-részecske,
amelyrõl Szillási Zoltánírása
szól - is igen sokfélék. A változatosságot
azonban még tovább növelik azon elméletek,
amelyek az elõttünk álló, a Standard Modell
által meg nem válaszolt és Cynolter Gáborcikkében
már felvázolt kérdéseket egy új
szimmetria, a szuperszimmetriafeltételezésével
kísérlik megválaszolni.
A szimmetriák
központi jelentõségűek a fizikában.
A szuperszimmetria, amely a részecskefizika hagyományos,
4 dimenziós kvantumtérelméleti leírásában
a lehetséges legtágabb szimmetria, összeköti
az anyagrészecskéket (a feles spinû fermionokat)
a kölcsönhatások közvetítõ részecskéivel
(az egész spinû bozonokkal), és eközben
új, szuperszimmetrikus részecskék bevezetését
követeli meg a szimmetria kiteljesítéséhez.
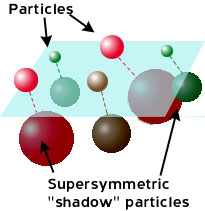
A
legegyszerûbb szuperszimmetrikus elmélet, a Minimális
Szuperszimmetrikus Standard Modell, a Standard Modell minden részecskéjéhez
egy szuperszimmetrikus részecskét, szuperpartnert
rendel (1. táblázat). A töltött leptonok
szuperpartnerei a töltött skalár leptonok vagy
röviden sleptonok(például a jól
ismert elektron társát skalár elektronnak vagy
selektronnak nevezzük), a neutrínóké a
sneutrínók, a kvarkoké a skvarkok.
A másik oldalról az elektrogyenge mértékbozonok
(a foton, a Z- és W-bozonok) valamint a Higgs-bozonok partnerei
a gaugínók2 (ejtsd:
gédzsínók), amelyeket töltésük
alapján megkülönböztetve chargínóknak3
(ejtsd: csardzsínók) vagy neutralínóknak
nevezünk, az erõs kölcsönhatás
színes gluonjaié pedig gluínók.

1. táblázat.
A Standard Modell részecskéi és szuperszimmetrikus
partnereik. l jelöli a három lepton családot
(e, m, t), q pedig a hat lehetségeskvarkot (d, u, s, c, b,
t). Az L (left) és R (right) indexek a részecskebal-
illetve jobbkezes voltára1 utalnak. A szuperszimmetrikusrészecskék
elnevezése a következõ módon történik:
a fermionok skalár (nulla spinû) partnerei az s-"
elõtagot, a bozonok fermion partnerei pedig az -ínó"
utótagot kapják. A szuperszimmetrikus részecskék
rövidjelölésben egy hullámvonalat kapnak.
Az azonos töltéssel és spinnel rendelkezõ
állapotok keveredhetnek. A keveredés eredményekéntkialakuló
tömegsajátállapotokat zárójelben
adtuk meg
A figyelmes olvasónak
szemet szúrhat egy eltérés. A Standard Modellen
túl címû cikkben a szuperpartnerek felsorolásánál
a következõk szerepelnek: fotínók,
zínó, wínó és higgsínó,
ehelyütt pedig chargínókat és neutralínókat
emlegettünk. A látszólagos ellentmondás
feloldása a keveredés jelenségében
rejlik, amelyrõl a Standard Modellt tárgyaló
írásban már olvashattak. A természetben
(reményeink szerint) megfigyelhetõ részecskék
azok, amelyek meghatározott tömeggel rendelkezõ
állapotoknak felelnek meg. E tömeg- sajátállapotok(chargínók
és neutralínók) a szuperpartner (azaz a fotínó,
zínó, wínó és higgsínó)
terek keveredésébõl állnak elõ.
Egy pillanatra vissza
kell térnünk a Higgs-bozonok rejtélyéhez.
A Standard Modellben az, hogy az elemi részecskék
tömeget kapjanak, csupán egyetlen semleges Higgs-bozon
létezését igényli. A szuperszimmetria
feltételezése azonban az elméletben fellépõ
Higgs-bozonok számának növekedését
eredményezi: az elmélet három semleges (h0,
H0, A0) és két töltött
(H+, H-) Higgs-bozon létét jósolja.
A szuperszimmetrikus
elméletek keretet adhatnak a hagyományos részecskefizikai
kölcsönhatások, azaz az elektromágneses,
a gyenge és az erõs kölcsönhatás,
valamint a gravitáció egyesített elméletbe
foglalására. A gravitációs kölcsönhatás
feltételezett közvetítõ részecskéjétgravitonnak
(G), szuperpartnerét pedig gravitínónak
( ) nevezzük.
A fentiekbõl
is kitûnik, hogy bár a szuperszimmetria feltételezése
elegánsan képes megválaszolni a részecskefizika
napjainkban nyitott kérdéseinek jelentõs részét,
nagy árat követel ezért: az elemi részecskék
száma több mint megkétszerezõdik, és
az elmélet paramétereirõl még nem is
ejtettünk szót...
) nevezzük.
A fentiekbõl
is kitûnik, hogy bár a szuperszimmetria feltételezése
elegánsan képes megválaszolni a részecskefizika
napjainkban nyitott kérdéseinek jelentõs részét,
nagy árat követel ezért: az elemi részecskék
száma több mint megkétszerezõdik, és
az elmélet paramétereirõl még nem is
ejtettünk szót...
Variációk
egy témára
 Ha
a szuperszimmetria a természet egzakt, nem sértett
szimmetriája lenne, akkor minden ismert részecskéhez
tartozna egy vele teljesen azonos tömegû szuperpartner.
Mivel azonban mindeddig egyetlen szuperpartnert sem fedeztünk
fel, a szuperszimmetriának sérülnie kell, ezzel
téve lehetõvé, hogy a részecskék
és partnereik tömege jelentõsen eltérhessen
egymástól. A hierarchia probléma1
megoldása a szuperszimmetria-sértés skálájára
az elektrogyenge fázisátalakuláshoz közeli
energiát kíván.
Ha
a szuperszimmetria a természet egzakt, nem sértett
szimmetriája lenne, akkor minden ismert részecskéhez
tartozna egy vele teljesen azonos tömegû szuperpartner.
Mivel azonban mindeddig egyetlen szuperpartnert sem fedeztünk
fel, a szuperszimmetriának sérülnie kell, ezzel
téve lehetõvé, hogy a részecskék
és partnereik tömege jelentõsen eltérhessen
egymástól. A hierarchia probléma1
megoldása a szuperszimmetria-sértés skálájára
az elektrogyenge fázisátalakuláshoz közeli
energiát kíván.
Az
elméleti fizikusok számára a szuperszimmetria-sértés
módja okozza a legnagyobb fejtörést. A Higgs-jelenség
leírásakor is tárgyalt spontán szimmetriasértésigen
közkedvelt és hatékony mechanizmus a részecskefizikában.
Szuperszimmetrikus elméletekben azonban legegyszerûbb
közvetlen megvalósításával problémák
lépnek fel, amelyek kikerülésére hagyományosan
feltételezzük, hogy létezik két elkülönülõ
szektor: egy látható,amely a Standard Modell
részecskéket (SM-részecskék) és
szuperpartnereiket tartalmazza, és egy rejtett, amelyben
a látható szektor részecskéivel nem
kölcsönható részecskék találhatók.
A szuperszimmetria spontán sérül az elektrogyenge
skálánál jelentõsen nagyobb energián,
a rejtett szektorban, és ennek a hatása jut át
valamilyen mechanizmus segítségével a látható
szektorba. Innen két út közül szokás
választani, amelyek a közvetítõ természetében
térnek el egymástól: az egyikben a gravitáció(ezeket
hívjuk szupergravitációs modelleknek),
a másikban pedig a mértékkölcsönhatásokjátsszák
el ezt a szerepet. A két modell, ahogy a késõbbiekben
látni fogjuk, igen eltérõ jóslatokat
ad, fõképpen a gravitínó tömegére,
és ezért kísérleti vizsgálatuk
eltérõ stratégiát követel.
Egy
másik jelentõs elágazási pont a mérések
optimalizálásánál az R-paritásmegmaradásának
feltételezése. Az R-paritás egy szorzódó
kvantumszám, amely az SM-részecskékre +1, azok
szuperpartnereire -1. Amennyiben feltételezzük az R-paritás
megmaradását, a szuperszimmetrikus részecskék
csak párosan szerepelhetnek a kölcsönhatásokban,
azaz csak párban keletkezhetnek. Bomlásuk kaszkád
jellegû, amelynek végeredményeként a
legkönnyebb szuperszimmetrikus részecske, amely e modellekben
szükségszerûen stabil, valamint SM-részecskék
keletkeznek. Ezzel ellentétben, ha az R-paritás nem
megmaradó kvantumszám, akkor a szuperszimmetrikus
részecskék keletkezhetnek egyedül. Mivel a legkönnyebb
szuperszimmetrikus részecske sem stabil, ezért pusztán
SM-részecskékre bomolhatnak.
Szót
kell még ejtenünk ehelyütt a paraméterekrõl.
A szuperszimmetrikus elméletek variánsait vizsgálva
további komplikációt jelent a fellépõ
paraméterek nagy száma, még a legtakarékosabb"
további feltételezések esetén is. A
paraméterek értékére nem léteznek
jóslatok, ellenben azok nagyban befolyásolják
a szuperszimmetrikus részecskék várható
tömegét, viselkedését.
A fentiekbõl
talán már látható, hogy nincs könnyû
dolga sem az elméleti, sem a kísérleti fizikusoknak:
az új, elméleti szempontból kívánatos
szimmetria feltételezése után még számtalan
lehetõség áll elõttünk, amelyek
megvalósulhatnak a természetben. A feladatunk az,
hogy átgondoltan sorra vegyük a lehetõségeket,
megvizsgáljuk, milyen mérhetõ hatásokra
számíthatunk, majd megmérjük azokat. Kísérleti
eredményeink gondos értelmezése adhatja csak
meg a választ a kérdésekre: Szuperszimmetrikus-e
a világ: valóban összeköti-e egy szimmetria
az anyagrészecskéket és a kölcsönhatások
közvetítõ részecskéit, ezzel bizonyos
szempontból egyesítve az anyagot és a természetben
jelen lévõ erõket? Ha így van, akkor
hogyan sérül a szuperszimmetria alacsony energiákon,
és melyek, mekkorák a természetet leíró
alapvetõ fizikai paraméterek?
A továbbiakban,
építve a Higgs-bozonok keresésérõl
szóló cikk bevezetõjére a részecskegyorsítókról
és detektorokról, közelebbrõl megvizsgáljuk
néhány példán keresztül, hogyan
próbáljuk megtalálni a szuperszimmetrikus részecskéket,
amelyek felfedezése megdönthetetlen kísérleti
bizonyítékul szolgálna mindannyiunk várakozására,
hogy a Standard Modellen túl egy új, elméleti
szempontból kielégítõbb modell vár
ránk.
Modellrõl
modellre: egy részecske nyomában4
 Minden
részecskekeresés megtervezésekor válaszolnunk
kell néhány alapvetõ kérdésre.
Minden
részecskekeresés megtervezésekor válaszolnunk
kell néhány alapvetõ kérdésre.
Adott
az eszköz, amellyel dolgozni szándékozunk, esetünkben
egy részecskeütköztetõ mellett felépített
detektor. Az elsõ kérdés: A gyorsító
által szolgáltatott részecskék kölcsönhatásakor
keletkezhet- e a keresett részecske, s ha igen, akkor
milyen folyamato(ko)n keresztül és milyen gyakorisággal?
Amennyiben
kitaláltuk a keletkezés módját, a következõ
lépés: Hogyan fog a keletkezett új részecske
viselkedni? Stabil avagy annak tekinthetõ, mivel élettartama
hosszabb, mint az az idõ, ami alatt elhagyja a detektor térfogatát?
Milyen nyomot hagy a detektorunkban, esetleg láthatatlanul
távozik? Ha elbomlik más részecskékre,
mikor teszi ezt: azonnal elbomlik, esetleg csak egy kis út
megtétele után? Milyen részecskékre
bomlik el?
Rajzoljunk kölcsönhatásokat!
A részecskefizikában a lejátszódó
folyamatok ábrázolására Feynman-diagramokat
használunk. Példaként tekintsük
az 1. ábrát, ahol a jól ismert elektron
nehezebb társa, a müon szuperpartnerének keletkezése
látható egy elektron-pozitron ütköztetõben.
A Feynman-diagramokon az idõ balról jobbra folyik,
azaz jelen esetben a történések egymásutánja
a következõ: egy felgyorsított elektron és
pozitron (az elektron antirészecskéje) találkozik
és kölcsönhatásuk eredményeként
egy virtuális foton vagy egy Z-bozon keletkezik, amely
ezután elbomlik egy pozitív és egy negatív
smüonra. Szokásosan a fermionokat folytonos, a Standard
Modell elektrogyenge szektorának vektorbozonjait hullámos,
a gluonokat feltekeredõ, a többi bozont pedig szaggatott
vonallal jelöljük. A fermion vonalakon a nyilak iránya
mondja meg, hogy részecskét avagy antirészecskét
jelölnek-e: a részecskék esetén az idõ
folyásával egyezõ, antirészecskéknél
azzal ellentétes irányba mutatnak. A vonalak találkozási
pontjait vertexeknek nevezzük, és egy csatolási
állandóval jellemezzük, amely a kölcsönhatás
erõsségére jellemzõ.
Érdekes
megemlíteni, hogy a Feynman-diagramok nem pusztán
a részecskék kölcsönhatásának
szemléltetésére szolgálnak: segítségükkel
egyszerû szabályok alapján felírható
a fizikai folyamatok hatáskeresztmetszete (vagy valószínûsége,
gyakorisága).
A
fenti kérdések megválaszolása után
már képet alkothatunk arról, mit is keresünk
a gyakorlatban... Vegyünk egy példát! Tegyük
fel, hogy a jól ismert elektron nehezebb társa,
a müon szuperpartnerét keressük egy elektron-pozitron
ütköztetõ mellett. Smüonok párban
keletkezhetnek egy virtuális5
foton vagy Z-bozon keletkezésén keresztül,
ahogy azt az 1. ábra mutatja. (A virtuális
részecskék nem figyelhetõk meg közvetlenül,
szinte azonnal - az energiára és idõre vonatkozó
Heisenberg-féle határozatlansági relációból
megbecsülhetõ élettartamuk lejárta után
- elbomolnak más részecskékre.)

1. ábra.
Smüonpárok keletkezése elektron-pozitron
ütközésben
Szupergravitációs,
R-paritás-õrzõ modellekben a legkönnyebb
szuperszimmetrikus részecske, amely - mint már
tudjuk - stabil, általában a legkönnyebb
neutralínó6. A kozmológiai
megfigyelések nem valószínûsítik
azokat a paramétertartományokat, ahol a legkönnyebb
szuperszimmetrikus részecske elektromosan töltött,
pl. a chargínó vagy a top-squark (röviden
stop).A neutralínó egy semleges részecske,
amely nem hagy nyomot a detektorban, így impulzusát,
energiáját nem tudjuk közvetlenül mérni.
Ezért a kijövõ (az ütközésben
keletkezõ) részecskék detektorban mért
teljes energiája kisebb lesz, mint a bejövõ
részecskék (példánkban az összeütközõ
elektron és pozitron) energiája. Ezekben a modellekben
tehát a szuperszimmetrikus részecskék keletkezését
a végállapot jelentõs energiahiánya
kíséri.
Térjünk
vissza a példánkban keletkezõ smüonok
bomlásához. A fenti modell szerint egy smüon
bomlásakor egy neutralínó és egy müon
keletkezik, a végállapotban két neutralínót
és két müont eredményezve. A neutralínók
észlelés nélkül távoznak a detektorból,
a müonok azonban jellegzetes nyomot hagynak. A 2. ábrán
egy Monte Carlo-programmal szimuláltsmüonpár
esemény látható két különbözõ
nézetben, ahogy a detektorban észlelnénk. A
részecskeütköztetõk mellett épített
detektorok legtöbbször hengerszimmetrikusak és
réteges felépítésûek. A 2.
ábrabal oldalán a smüonpár esemény
a beérkezõ elektronnyaláb irányából
látható. A körök a különbözõ
detektorelemeket szemléltetik. Az ábra közepébõl
induló vonalak a müonok nyomát mutatják
a nyomkövetõ detektorban.A következõ
rétegekben látható kockák" a kaloriméterekbenleadott
energiával arányosak, a nyilak pedig a legkülsõ
müondetektorbanészlelt beütésekre
utalnak. Azábra jobb oldalán az esemény az
elõzõre merõlegesen, oldalról látható.

2. ábra. Szimulált smüonpár
esemény 189 GeV tömegközépponti energián,
ahogy a detektorban észlelnénk, két különbözõ
nézetbõl. A Monte Carlo-számítás
elvégzésekor feltételeztük, hogy a smüon
tömege 90 GeV és a bomlásakor keletkezõ
neutralínóé 85 GeV
Mindeddig
feltételeztük, hogy az R-paritás megmarad, azaz
a folyamatokban a szuperszimmetrikus részecskék párosan
szerepelhetnek csak. Mivel azonban az R-paritás megmaradására
nincs sem elméleti, sem kísérleti bizonyíték,
igen fontos az R-paritás-sértõ folyamatok tanulmányozása
is, különösen ha tekintetbe vesszük azt, hogy
bizonyos R-paritás-sértõ bomlások valószínûsége
vetekedhet a hagyományos R-paritás-õrzõ
módusokéval.
Mi
történhet vajon az elõzõ oldalakon már
közelrõl megismert smüonokkal R-paritás-sértést
megengedõ elméletekben?
Ha a smüon nehezebb, mint a neutralínó, akkor
ebben az esetben is elbomolhat egy neutralínóra
és egy müonra. Azonban ez esetben semmi sem garantálja,
hogy a neutralínó stabil részecske legyen7,
elbomolhat ismert SM-részecskékre, amelyek (a neutrínó
kivételével) kölcsönhatásba lépnek
a detektor anyagával. Egy ilyen folyamat Monte Carlo-szimulációja
látható a 3. ábrán. A két
nyíllal jelzett müonnyom mellett most megjelennek
a neutralínó bomlásából származó
részecskék is, amelyek jóval bonyolultabbá
teszik a végállapotot.

3. ábra.
Szimulált smüonpár esemény R-paritás-sértést
megengedõ modellben 189 GeV tömegközépponti
energián, ahogy a detektorban észlelnénk,
két különbözõ nézetbõl.
A Monte Carlo-számítás elvégzésekor
feltételeztük, hogy a smüon tömege 94
GeV és a bomlásakor keletkezõ, kvarkokra
bomló neutralínóé 89 GeV
A fenti
bomláson kívül teljesen új lehetõségek
is állnak smüonunk elõtt: elbomolhat két
SM-fermionra, például két leptonra, egy
leptonra és egy kvarkra vagy két kvarkra. Ha mindkét
smüon kvarkokra bomlik, a végállapotban a
kvarkok hadronizációjából keletkezõ
négy részecskezáport1észlelhetnénk
detektorunkkal.
A
bevezetésben szót ejtettünk még azon
modellekrõl, amelyekben a szuperszimmetria-sértést
mértékkölcsönhatások közvetítik
a rejtett szektorból a láthatóba. Ezeket
a modelleket az angol elnevezés (Gauge Mediated Supersymmetry
Breaking) rövidítését használva
GMSB-vel jelöljük. GMSB-modellekbena legkönnyebb
szuperszimmetrikus részecske a gravitínó,
és a második legkönnyebb részecske -
amely fontos szerepet játszik a kísérleti
keresésben - vagy az egyik neutralínó vagy
a stau.
A
teljesség kedvéért vessünk ismét
egy pillantást a smüonpár eseményekre.
GMSB-modellekben a smüonok bizonyos feltételek teljesülése
esetén szintén elbomolhatnak egy neutralínóra
és egy müonra.
A keletkezõ neutralínó
lehet hosszú élettartamú, ekkor a 2. ábránláthatóhoz
hasonló végállapotot kapunk; vagy elbomolhat
egy gravitínóra és egy fotonra. Mivel a gravitínó
semleges, a detektort nyom nélkül elhagyó részecske,
a detektorunkkal ebben az esetben két müont és
két fotont észlelnénk, valamint energiahiányt
tapasztalnánk. A smüon elõtt álló
másik út, hogy egy gravitínóra és
egy müonra bomoljon el, és ismét a 2. ábrán
láthatóhoz hasonló végállapotot
eredményezne. Tovább bonyolíthatja a képet,
hogy a smüon élettartamának függvényében
a bomlás esetleg csak a detektor külsõ részében
történik meg, és ekkor egy megtört
nyomot láthatunk, vagy akár a detektoron kívül
is végbe mehet, két darab, egy egyenesbe esõ,
erõsen ionizáló nyomot adva.
Mit tanulhattunk
a fenti példákból?
 Egy
keresett részecske különbözõ modellekben,
illetve egy kiválasztott modell különbözõ
paramétertartományaiban igen különbözõ
módon viselkedhet (példáinkat a 4. ábrán
foglaltuk össze). Szerencsére egy adott modell adott
paraméterei esetén - elméleti fizikus kollégáink
munkájának hála - elég pontos jóslatok
állnak rendelkezésünkre, amelyek alapján
méréseink megtervezhetõk, optimalizálhatók.
Szisztematikusan, ám minden újra nyitott szemmel kell
dolgoznunk: modelljeink közül csupán egyetlen valósulhat
meg a természetben, és még az elméletek
e gazdagságában sem lehetünk biztosak abban,
hogy már köztük van az igazi.
Egy
keresett részecske különbözõ modellekben,
illetve egy kiválasztott modell különbözõ
paramétertartományaiban igen különbözõ
módon viselkedhet (példáinkat a 4. ábrán
foglaltuk össze). Szerencsére egy adott modell adott
paraméterei esetén - elméleti fizikus kollégáink
munkájának hála - elég pontos jóslatok
állnak rendelkezésünkre, amelyek alapján
méréseink megtervezhetõk, optimalizálhatók.
Szisztematikusan, ám minden újra nyitott szemmel kell
dolgoznunk: modelljeink közül csupán egyetlen valósulhat
meg a természetben, és még az elméletek
e gazdagságában sem lehetünk biztosak abban,
hogy már köztük van az igazi.

4. ábra. Smüonok keletkezése és bomlása
elektron-pozitron ütközésben, különbözõ
szuperszimmetrikus modellekben: a) R-paritás-õrzõ
szupergravitációs modell; b) R-paritás-sértõ
szupergravitációs modell - neutralínón
keresztüli közvetett bomlás; c) R-paritás-sértõ
szupergravitációs modell - közvetlen bomlás
a Standard Modell fermionjai; d) GMSB-modell - neutralínón
keresztüli közvetett bomlás; e) GMSB-modell -
közvetlen bomlás gravitínóra és
müonra. Az ábrákon fi-vel a Standard
Modell fermionjai (kvarkokat és/vagy leptonokat) jelöltünk
A
keresés hétköznapjai
Van
egy elméletünk, ennek segítségével
ismerjük a jóslatokat arra, milyen részecskék
jelenhetnek meg, és azok hogyan viselkednek detektorunkban.
A feladatunk: megtalálni õket, ha valóban léteznek
és a várakozásunknak megfelelõek, avagy
minél pontosabb megszorításokat adni a modellre,
a lehetséges paramétertartományokra, ha keresésünk
negatív eredményt ad.
Ahogy
már említettük, méréseinket, adataink
feldolgozását Monte Carlo-szimulációk
segítségével optimalizáljuk. Miután
képet kaptunk arról, hogy a keresett folyamat, továbbiakban
a jel, milyen tulajdonságokkal rendelkezik, számba
kell vennünk, hogy milyen más fizikai folyamatok adhatnak
ehhez hasonló végállapotokat. Ezeket a mérésünk
szempontjából zavaró eseményeket nevezzük
háttérnek.
A jel-
és a háttéresemények részletes
összehasonlítása segít a megfelelõ
válogatási kritériumokmegállapításához8,
amelyek segítségével eldobhatjuk a háttér,
és kiválaszthatjuk a jel eseményeit, amennyiben
azok valóban jelen vannak. A kiválogatás után
a szimulációkból ismerjük a még
megmaradó háttéresemények várható
számát, valamint azt, hogy milyen hatásfokkal
vagyunk képesek kiválasztani a jeleseményeket,
és ez utóbbinak a segítségével
egy adott modell keretében kiszámolhatjuk a jelesemények
várható számát is.
E
ponton nyúlunk a detektorunk által gyûjtött
adatokhoz, végrehajtva azon a Monte Carlo-szimuláció
segítségével kidolgozott eseményválogatást.
Ha a kapott eredmény (lásd példaként
az 5.ábrát) konzisztens9
a jel + háttér" feltételezéssel,
akkor egy új felfedezés kapujába értünk;
ha azonban az észlelt események a csak háttér"
feltételezést támasztják alá,
akkor ez a sokszor negatívnak nevezett eredmény nyújt
lehetõséget arra, hogy korlátokat határozzunk
meg a modell paramétereire.

5. ábra.
Példaként megmutatjuk két azonos skalár
részecske 4. c ábrához hasonló bomlását
feltételezõ, végállapotban négy
részecskezáport tartalmazó események
kiválogatásának eredményét 189
GeV tömegközépponti energián. A vízszintes
tengelyen a feltételezett skalárrészecske tömegét
ábrázoltuk a részecskezáporok mért
négyesimpulzusából számolva, míg
a függõleges tengelyen az 1,5 GeV-es tömegtartományokban
észlelt események számát. A pontok a
hibákkal a kísérleti adatokra vonatkoznak,
a fehér és a sötétszürke hisztogramok
a Standard Modell különbözõ folyamataiból
eredõ, Monte Carlo-szimulációk segítségével
becsült hátteret mutatják, míg a világosszürke
hisztogrampárban keletkezõ 65 GeV tömegû
részecskék jelenléte esetén várható
többletet mutatja egy lehetséges paraméterkombináció
esetén. Errõl az ábráról szabad
szemmel is megjósolható, a statisztikai módszerek
segítségével pontosan megkapható eredmény,
hogy a kísérleti adatok ez esetben a csak háttér"
feltételezést támogatják
Ahogy talán
már sejthetõ, a munka még nem ért véget:
mindeddig nem fedeztünk fel egyetlen Standard Modellen túli
részecskét sem, azaz nem találtuk meg a közvetlen
kísérleti bizonyítékot arra, hogy világunk
gazdagabb a Standard Modell által leírtaknál.
A hátralévõ néhány sorban megpróbálom
(a terület szerteágazó volta miatt) a teljesség
igénye nélkül összefoglalni az eddigi méréseket
és röviden felvázolni az elõttünk
álló lehetõségeket.
Ahol most
tartunk
 Napjainkban
elsõsorban három nagy gyorsító segítségével10
kutatják új részecskék keletkezését.
Napjainkban
elsõsorban három nagy gyorsító segítségével10
kutatják új részecskék keletkezését.
Elsõként
a Genf mellett mûködõ Európai Részecskefizikai
Laboratórium (CERN) 200 GeV tömegközépponti
energiát meghaladó elektron-pozitron ütköztetõjérõl,
a LEP-rõl ejtünk szót. Azelektron-pozitron ütközés
tiszta környezete igen jó lehetõséget
teremt szinte minden szuperpartner keresésére. Az
elmúlt évek során mind az adott modelleket
megcélzó, mind a végállapotok topológiájából
kiinduló (több-kevésbé) modellfüggetlen
analízisek is születtek. A LEP eredményei alapján
a legtöbb szuperszimmetrikus részecske tömegére
a Z-bozon tömege körüli alsó határt
állapítottunk meg, igaz, gyakorta csak bizonyos mellékfeltételek
teljesülése esetén. Jelenleg a leggyengébb
korlátok a sneutrínók és a legkönnyebb
neutralínó tömegére állnak fenn.
Bár
a LEP-kísérletek a modellek és azok paramétereinek
igen széles skáláját képesek
vizsgálni, az általuk elérhetõ legnagyobb
részecsketömegek nem vehetik fel a versenyt a Chicago
közelében mûködõ Tevatron proton-antiproton
gyorsítónál tanulmányozhatókéval.
A CDF és D0 kísérletek 1,8 TeV tömegközépponti
energián11 gyûjtött
adatait mind szupergravitációs, mind GMSB-modellek
keretében vizsgálták.
A
hadron ütköztetõk zavaros" eseményei12
(6. ábra)csak bizonyos típusú végállapotok
vizsgálatát teszik lehetõvé. A klasszikus
analízisek nagy transzverzális13
energiájú objektumokat (fotonokat, leptonokat, hadronzáporokat
vagy éppen hiányzó energiát) követelnek
meg. A legfontosabb eredményeiket a skvarkok (fõként
a stop), a gluínó és a gaugínó
keltésének vizsgálata adja.

6. ábra.
A Tevatron gyorsító mellett mûködõ
CDF detektorral észlelt proton-antiproton ütközés.
A bal oldalon a nyaláb irányából nézve
láthatóak a detektorban észlelt beütések,
míg a jobb oldalon az elektromágneses kaloriméter
kiterített" képén látható
az észlelt transzverzális energia nagysága.
Mindkét ábrázolási módban jól
látható az érdekes" folyamatból származó
négy nagy energiájú részecske mellett
megjelenõ sok egyéb részecske
A
hamburgi DESY kutatóközpont elektron-proton ütköztetõje,
a HERA, 320 GeV tömegközépponti energián
mûködik és egyedülálló nyalábkombinációjának
hála egyes csatornák (például R-paritás-õrzõ
modellekben egy selektron és egy skvark együttes keletkezése
eq ®
 , vagy R-paritás-sértõ modellekben egy skvark
keletkezése eq ®
, vagy R-paritás-sértõ modellekben egy skvark
keletkezése eq ® hatékony vizsgálatára ad módot.
A
felsorolt keresések egyike sem mutatott ki határozott
eltérést a Standard Modell várakozásaitól,
így csupán"határokat tudtunk megállapítani
az elméletek paramétereire. A hagyományos
szuperszimmetrikus elméletek minimalista" változatai
erõsen korlátok közé szorítottak,
ám általánosságban a szuperszimmetria
még a már elérhetõ kinematikus tartományban
is rejtõzhet.
hatékony vizsgálatára ad módot.
A
felsorolt keresések egyike sem mutatott ki határozott
eltérést a Standard Modell várakozásaitól,
így csupán"határokat tudtunk megállapítani
az elméletek paramétereire. A hagyományos
szuperszimmetrikus elméletek minimalista" változatai
erõsen korlátok közé szorítottak,
ám általánosságban a szuperszimmetria
még a már elérhetõ kinematikus tartományban
is rejtõzhet.
Amit a
jövõ tartogat
 A
CERN LEP gyorsítója 12 év után idén
fejezi be mûködését, elérve legmagasabb
tömegközépponti energiáját, mintegy
210 GeV-et. Talán kevesen számítanak már
meglepetésekre, de a tudománytörténet
tanulsága és sokunk reménye szerint még
az utolsó nekifutás adatainak feldolgozása
is meghozhatja az elsõ sorsdöntõ eredményeket.
A
CERN LEP gyorsítója 12 év után idén
fejezi be mûködését, elérve legmagasabb
tömegközépponti energiáját, mintegy
210 GeV-et. Talán kevesen számítanak már
meglepetésekre, de a tudománytörténet
tanulsága és sokunk reménye szerint még
az utolsó nekifutás adatainak feldolgozása
is meghozhatja az elsõ sorsdöntõ eredményeket.

A LEP-tõl
a stafétabotot14 a Chicago
közelében mûködõ 2 TeV energiájú
proton-antiproton gyorsító, a Tevatron 2001-ben kezdõdõ
új mérési szakasza veszi át, amely jelentõsen
átépített, még nagyobb érzékenységû
detektoraival, valamint a következõ években várható
nagy luminozitásával jó esélyekkel indul
a nemes versengésben az elsõként felfedezett,
nem SM-részecskéért.
Amennyiben
sem a LEP, sem a Tevatron nem hozza meg a várva várt
áttörést, 2005-ben a CERN LHC (Large Hadron Collider)
gyorsítóján a sor. Ez a 14 TeV tömegközépponti
energiájú gyorsító lesz az évtized
részecskefizikai berendezése, amely végleg
tisztázhatja az elektrogyenge szimmetriasértés
körüli kérdéseket: léteznek- e
Higgs-bozonok, és ha igen, milyenek? valamint választ
adhat arra is: szuperszimmetrikus-e a természet?Ugyanis
ha a szuperszimmetria a válasz a hierarchiaproblémára,
akkor az 1 TeV skála környékén meg kell
találnunk az elsõ szuperpartnereket.
Izgalmas
és - akár pozitív, akár negatív
válaszokat kapunk kérdéseinkre - mindenképpen
sorsdöntõ évek állnak elõttünk.
Könnyen elõfordulhat, hogy az elsõ új
részecskét egy ma még csak a fizikát
tanuló diák látja" megmajd számítógépe
képernyõjén.
Mi is ott
lehetünk
 A
Standard Modellen túli fizika kísérleti keresésében
magyar diákok, fizikusok is évek óta részt
vesznek15 a CERN LEP gyorsítója
mellett mûködõ két nagy nemzetközi
együttmûködés, az L3- és az OPAL-kísérletek
keretében16. Bár a LEP
gyorsító idén befejezi mûködését,
hogy átadja helyét az új, nagy reményekre
jogosító LHC-nek, a lehetõség továbbra
is a miénk. Magyarország CERNtagsága, és
az a tény, hogy aktív részesei vagyunk az LHC
CMS (Compact Muon Solenoid) detektora elõkészítési,
fejlesztési, építési munkálatainak,
biztosítja számunkra, hogy kutatásainkat a
következõ évtized egyik részecskefizikai
csúcskísérletében folytathassuk.
A
Standard Modellen túli fizika kísérleti keresésében
magyar diákok, fizikusok is évek óta részt
vesznek15 a CERN LEP gyorsítója
mellett mûködõ két nagy nemzetközi
együttmûködés, az L3- és az OPAL-kísérletek
keretében16. Bár a LEP
gyorsító idén befejezi mûködését,
hogy átadja helyét az új, nagy reményekre
jogosító LHC-nek, a lehetõség továbbra
is a miénk. Magyarország CERNtagsága, és
az a tény, hogy aktív részesei vagyunk az LHC
CMS (Compact Muon Solenoid) detektora elõkészítési,
fejlesztési, építési munkálatainak,
biztosítja számunkra, hogy kutatásainkat a
következõ évtized egyik részecskefizikai
csúcskísérletében folytathassuk.
JEGYZETEK
1. Építünk,
ill. hivatkozunk Horváth Dezsõ,
Cynolter Gábor és Szillási
Zoltán cikkeinek egyes részeire, így
az érdeklõdõ olvasónak különös
figyelmébe ajánljuk ezeket az írásokat.
2. A mérték szó angol megfelelõjébõl
(gauge) képzett szó, amelyet magyarra mértékínóként
fordíthatnánk.
3. A töltés szó angol megfelelõjébõl
(charge) képzett szó, amelyet magyarra töltínóként
fordíthatnánk.
4. A továbbiakban csupán olyan
kísérletekrõl, mérésekrõl
ejtünk szót, amelyek nagy energiájú
részecskegyorsítók segítségével
folynak, és amelyek új részecskék
közvetlen kimutatását tûzték ki
célul. Mind maguk a gyorsítók, mind a mellettük
felépülõ nagy detektorok tervezése és
megépítése fizikusok és mérnökök
százainak hosszú évekig tartó közös
munkájának a gyümölcse. E nehéz,
de izgalmas folyamat felvázolása kívül
esik cikkünk lehetõségein, annyit azonban meg
kell említenünk, hogy egy új berendezés
alapötletének felvetésétõl a
részletek aprólékos kidolgozásáig
a fizikusok szeme elõtt a vizsgálandó legfontosabb
fizikai folyamatokra való érzékenység
és a késõbbi minél szélesebb
körû alkalmazhatóság lebeg.
5. Virtuálisnak nevezünk egy részecskét,
ha az nem a tömeghéjon keletkezik, vagyis négyes-impulzusából
számolható tömege nem egyezik meg a részecskét
jellemzõ tömeggel (például egy virtuális
foton tömegére nullától különbözõ
értéket kapnánk).
6. Egyes paraméter-tartományokban
a legkönnyebb szuperszimmetrikus részecske az egyik
sneutrínó.
7. Pontosabban szólva, az R-paritás-sértõ
vertexekhez tartozó csatolások értékének
függvénye a szuperszimmetrikus részecskék
(jelen esetben a neutralínó) élettartama.
Kellõen nagy, ám más mérések
(pl. a proton-bomlás vizsgálata) által még
nem kizárt értékeket véve a szuperszimmetrikus
részecskék elbomlanak a detektor térfogatában.
8. Egy ilyen kritérium lehet például
az eseményben található részecskék
számának, a detektorban észlelt teljes energia
nagyságának vagy a napjainkban igen közkedvelt
mesterséges ideghálózatok segítségével
több jellemzõ fizikai mennyiség kombinációjaként
kapott érték korlátozása.
9. Ennek a kérdésnek az eldöntésére
a valószínûség-számítás
módszereit hívjuk segítségül.
10. Nem fontosságuk, csupán a
cikk kereteinek szûkössége miatt nem ejtünk
szót azokról a kísérletekrõl,
amelyekben egy céltárgyat bombáznak felgyorsított
részecskenyalábbal.
11. Proton-antiproton ütközésekben
nem áll a teljes tömegközépponti energia
rendelkezésre új részecskék keltésére,
mivel a proton ill. az antiproton összetett részecske
és energiája megoszlik az õt felépítõ
kvarkok között.
12. Gondoljunk csak arra, hogy az esetlegesen
megjelenõ szuperszimmetrikus részecskék jó
esetben is csak a proton ill. az antiproton egyetlen kvarkját
használják el, így ennek maradéka
detektorunkban megjelenve elrejtheti elõlünk az érdekes
folyamatot, az új részecske keletkezését.
13. A nyaláb irányára merõleges
vetületben számolt.
14. Ahogy az elõzõ szakaszban
megemlítettük, a Tevatron már eddig is számos
értékes eredményt adott a részecskefizikának.
15. A kutatásokat az Országos
Tudományos Kutatási Alap az OTKA F023259, T019181,
T023793, T024011 és T029328 számú szerzõdések
alapján támogatja.
16. A szerzõ maga is e témakörben,
töltött Higgs-bozonok és szuperszimmetrikus részecskék
R-paritássértõ bomlásainak keresésérõl
írta PhD-értekezését az OPAL detektor
adatainak felhasználásával. esemény
|
Véletlenszámok a tudomány szolgálatában
 A
részecskefizikában használt berendezések,
mérések tervezésekor, illetve késõbb,
az összegyûjtött adatok feldolgozásakor
az egyik legfontosabb eszköz a Monte Carlo-szimuláció.
A Monte Carlo-módszer igen széles körben
(a pénzügyi élettõl a bonyolult
rendszerek kockázatanalízisén át
az alaptudományokig) alkalmazott numerikus eljárás,
amely véletlenszámok generálásán
alapul. Az elnevezés - a szerencsejátéko(so)k
városa - a statisztikus szimuláció és
a szerencsejátékok közti hasonlóságra
utal. Egy fizikai (matematikai) rendszer gyakran jellemezhetõ
valószínûség- eloszlásokkal.
Ha ismerjük ezeket az eloszlásokat, a Monte Carlo-szimuláció
azonnal elvégezhetõ véletlen mintavételezéssel.
A mintavételezést sokszor elvégezve kiátlagolhatjuk
a kapott eredményeket, és megbecsülhetjük
az átlag hibáját. Megválaszolhatjuk
a kérdést, hogy az adott mennyiség az
esetek milyen hányadában halad meg egy adott
értéket, esik egy ismert intervallumba... Szemléltetésül
nézzük meg, hogyan készülhet egy szimulált
smüonpár esemény. Elsõ lépésként
feltételezéseket kell tennünk az elmélet
paramétereire, hiszen ezek határozzák
meg, mekkora lesz a smüon tömege, lejátszódhat-e
az adott folyamat, és ha igen, akkor milyen valószínûséggel.
Ezután már valóban hozzákezdhetünk
a feladathoz. Példánkban a beérkezõ
elektron és pozitron energiája megegyezik a
nyalábenergiával, impulzusuk azonos nagyságú,
de ellenkezõ irányú, így az energia-
és impulzusmegmaradás törvénye szerint
a virtuális foton vagy Z-bozon nyugalomban, kétszeres
nyalábenergiával keletkezik. Az elmélet
paramétereinek ismeretében meghatározhatjuk
annak a valószínûségét,
hogy a közbensõ bozon egy smüonpárra
bomlik el. Tegyük fel, hogy Fortuna és a véletlenszám-
generátor kegyeltjei vagyunk, és valóban
egy smüonpár jön létre az eseményünkben.
(Ha nem így történne, akkor addig próbálkozunk,
amíg ránk nem mosolyog a szerencse.) Ismerve
a smüonok tömegét (a pozitív és
a negatív töltésû smüon tömege
megegyezik, hiszen egymás antirészecskéi),
kiszámolhatjuk energiájukat és impulzusuk
nagyságát. Azonban impulzusuk irányát
egy valószínûség-eloszlás
írja csak" le, így ismét szükségünk
van egy véletlenszámra, amely megmondja nekünk,
az adott eseményben merre is menjenek a részecskék.
A következõ lépés a smüonok
elbomlasztása, amelyet az elõzõekhez
hasonlóan végzünk el. Ha ezzel készen
vagyunk, akkor már ismerjük a végállapotban
lévõ részecskéket, és a
feladatunk e részecskék és a detektor
anyaga közti kölcsönhatás leírása
lesz, szintén valószínûség-eloszlások
és véletlenszámok segítségével.
A Monte Carlo-módszer legnagyobb elõnye, hogy
nincs szükség a sokszor igen bonyolult rendszer
analitikus vagy hagyományos numerikus módszerekkel
történõ megoldására, hanem
csupán" véletlenszámok gyors és
hatékony generálásával megválaszolhatók
a feltett kérdések, megoldható a probléma. A
részecskefizikában használt berendezések,
mérések tervezésekor, illetve késõbb,
az összegyûjtött adatok feldolgozásakor
az egyik legfontosabb eszköz a Monte Carlo-szimuláció.
A Monte Carlo-módszer igen széles körben
(a pénzügyi élettõl a bonyolult
rendszerek kockázatanalízisén át
az alaptudományokig) alkalmazott numerikus eljárás,
amely véletlenszámok generálásán
alapul. Az elnevezés - a szerencsejátéko(so)k
városa - a statisztikus szimuláció és
a szerencsejátékok közti hasonlóságra
utal. Egy fizikai (matematikai) rendszer gyakran jellemezhetõ
valószínûség- eloszlásokkal.
Ha ismerjük ezeket az eloszlásokat, a Monte Carlo-szimuláció
azonnal elvégezhetõ véletlen mintavételezéssel.
A mintavételezést sokszor elvégezve kiátlagolhatjuk
a kapott eredményeket, és megbecsülhetjük
az átlag hibáját. Megválaszolhatjuk
a kérdést, hogy az adott mennyiség az
esetek milyen hányadában halad meg egy adott
értéket, esik egy ismert intervallumba... Szemléltetésül
nézzük meg, hogyan készülhet egy szimulált
smüonpár esemény. Elsõ lépésként
feltételezéseket kell tennünk az elmélet
paramétereire, hiszen ezek határozzák
meg, mekkora lesz a smüon tömege, lejátszódhat-e
az adott folyamat, és ha igen, akkor milyen valószínûséggel.
Ezután már valóban hozzákezdhetünk
a feladathoz. Példánkban a beérkezõ
elektron és pozitron energiája megegyezik a
nyalábenergiával, impulzusuk azonos nagyságú,
de ellenkezõ irányú, így az energia-
és impulzusmegmaradás törvénye szerint
a virtuális foton vagy Z-bozon nyugalomban, kétszeres
nyalábenergiával keletkezik. Az elmélet
paramétereinek ismeretében meghatározhatjuk
annak a valószínûségét,
hogy a közbensõ bozon egy smüonpárra
bomlik el. Tegyük fel, hogy Fortuna és a véletlenszám-
generátor kegyeltjei vagyunk, és valóban
egy smüonpár jön létre az eseményünkben.
(Ha nem így történne, akkor addig próbálkozunk,
amíg ránk nem mosolyog a szerencse.) Ismerve
a smüonok tömegét (a pozitív és
a negatív töltésû smüon tömege
megegyezik, hiszen egymás antirészecskéi),
kiszámolhatjuk energiájukat és impulzusuk
nagyságát. Azonban impulzusuk irányát
egy valószínûség-eloszlás
írja csak" le, így ismét szükségünk
van egy véletlenszámra, amely megmondja nekünk,
az adott eseményben merre is menjenek a részecskék.
A következõ lépés a smüonok
elbomlasztása, amelyet az elõzõekhez
hasonlóan végzünk el. Ha ezzel készen
vagyunk, akkor már ismerjük a végállapotban
lévõ részecskéket, és a
feladatunk e részecskék és a detektor
anyaga közti kölcsönhatás leírása
lesz, szintén valószínûség-eloszlások
és véletlenszámok segítségével.
A Monte Carlo-módszer legnagyobb elõnye, hogy
nincs szükség a sokszor igen bonyolult rendszer
analitikus vagy hagyományos numerikus módszerekkel
történõ megoldására, hanem
csupán" véletlenszámok gyors és
hatékony generálásával megválaszolhatók
a feltett kérdések, megoldható a probléma.
forrás
|













Kommentáld!