Az időszámítás alapja a suméroknál három égitest mozgása volt: a Föld tengelyforgása (ez adja a napok számát) a Hold keringése a Föld körül (hónap) és a Föld keringése a Nap körül (év).

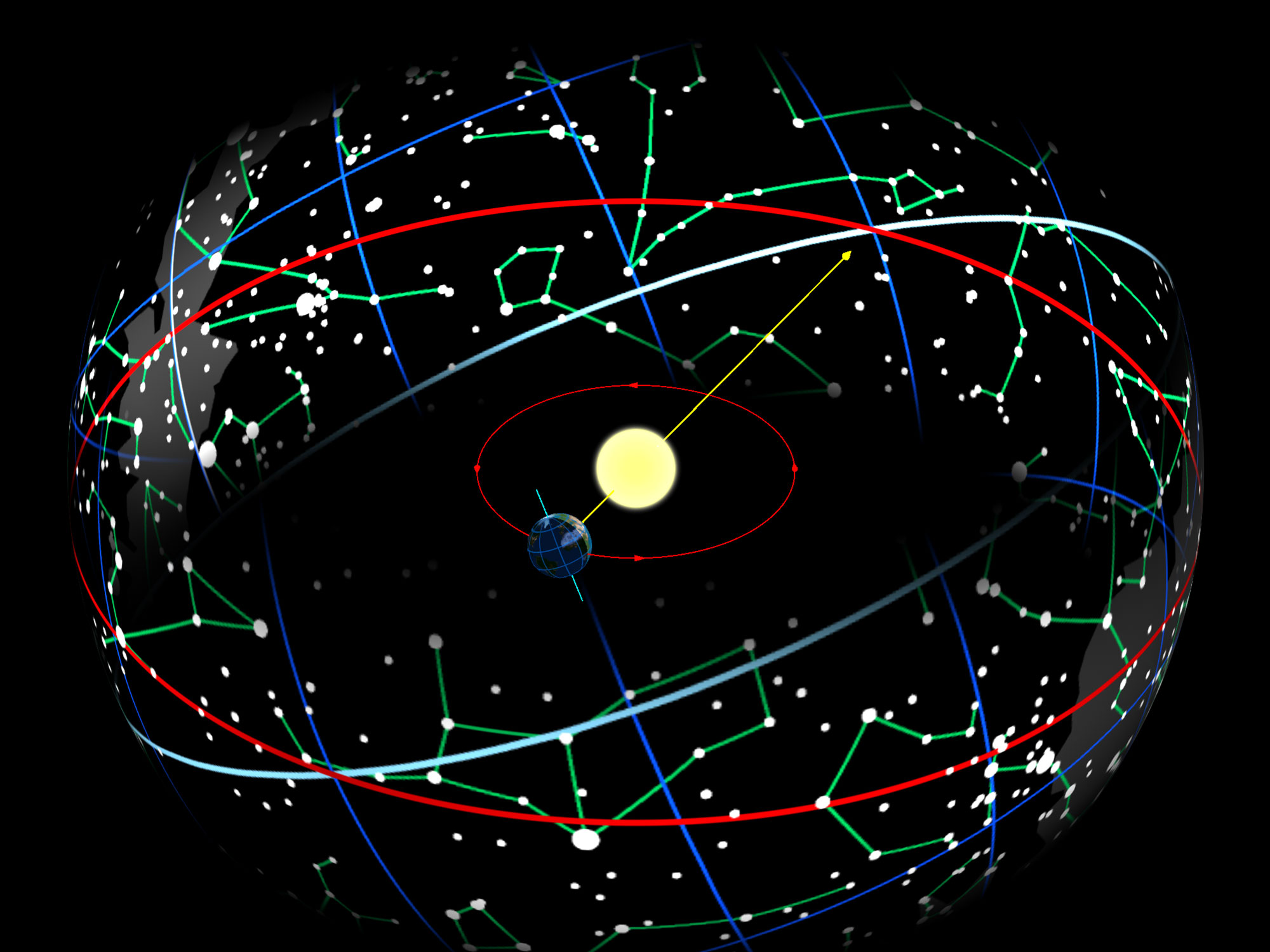
Mivel ez a három mozgás csak igen közvetett kapcsolatban van egymással, ezért időtartamuk is független egymástól. Ha alapegységül a Föld tengelyforgásának idejét vesszük, és ezt vesszük egy napnak, sem a hónap sem az év nem határozható meg racionális számmal kifejezhető napokkal, sem az évet alkotó holdhónapok száma sem racionális szám. Ezek az időegységek tehát nem többszörösei egymásnak, és összemérhetetlen mennyiségek is.

Így tehát minden naptári rendszer csak megközelítő pontosságú. Az, hogy milyen módszert alkalmazunk a matematikailag összemérhetetlen időegységek egyeztetésére, hogy a természetes en adott alapegység, a nap mellett viszonylag milyen jelentőséget tulajdonítunk a holdhónapnak, illetve a napévnek - ezek a tények határozzák meg egy-egy naptári rendszer jellegét.

A naptáralkotóknak a holdhónap napokra való átszámítása jelentette a legkisebb nehézséget. Kiindulva a holdhónapok 28 nap, 12 óra 44 perces átlagából, váltakozva 29 és 30 napos hónapokat kaptak. A havi 44 perces többlet egy évben kb. 9 órát tett ki, ez 8 év alatt 3 napra növekedett. Így egyes hónapoknak bizonyos években való egy napos meghosszabbításával elérték a gyakorlati szempontból kielégítő pontosságot.

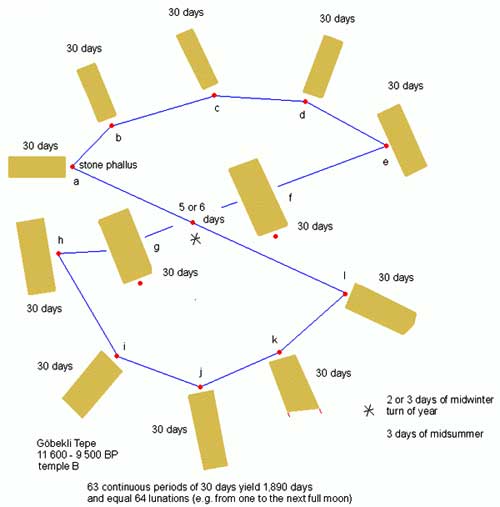
Nagyobb nehézséget jelentett a napév és a holdhónap egyeztetésének feladata. Egy napév igen durva megközelítéssel 12 holdhónapnak felel meg, de ez csak hozzávetőleges értékű, a hiba ugyanis évente 11 napot ér el. Az eltérés okozta nehézségeket meg lehet oldani úgy, hogy bizonyos években a 12 holdhónaphoz egy 13.-at (szökőhónapot) iktatunk be, és íly módon a hold járását hozzáigazítjuk a napévhez. Így jött létre a luniszoláris naptári rendszer. (A másik két módszer: szoláris: lemond a holfázisok figyelembevételéről és a nap járása alapján határozza meg az időegységet. Végül lehetséges a nap járásától teljesen függetlenül csak holdévekkel számolni. Eredménye a tisztán lunáris naptári rendszer.)

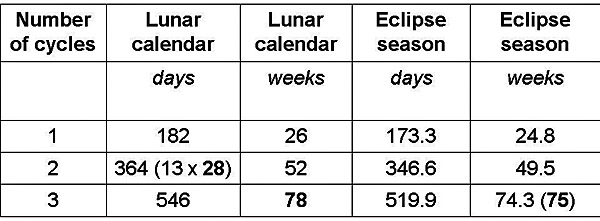
A sumér naptári rendszer luniszoláris jellegű volt. Ezen a naptári rendszeren alapult a zsidó (a zsinagógai naptár ma is luniszoláris) és görög naptár, a Ceasar reformja előtti római naptár, és ilyen volt a kínai naptár is.

A holdhónapok és a napév egyeztetéséhez szükséges szökőhónapok beiktatása - intercalatio - kezdetben a mindenkori gyakorlati szükségletnek megfelelően történt. Alkalmilag maga a király rendelte el egy-egy szökőhónap beiktatását. Természetesen a papok számításai és tanácsa alapján. Legtöbbször csillagászati jelenségek alapján döntöttek az év meghosszabbításáról.

A mezopotámiai naptár szerint a tavaszi napfordulónak (március 21.) az év első hónapjára, az őszinek az év hetedik hónapjára kellett esnie. Mikor a tavaszpont már a második hónapra esett volna, akkor elrendelték a 13. szökőhónap beiktatását. Idővel az alkalmi kiigazításokat felváltotta egy olyan rendszer, amikor az évek ciklusán belül meghatározott sorrendben követték egymást a 12 hónapos rendes, és a 13 hónapos szökőévek. Először 8 éves ciklust használtak, később a babiloni korban már 19 éves ciklussal számoltak, melyben 12 rendes és 7 szökőévet (13 hónapos év) helyeztek el. A 13. hónapot általában a tavaszpontot megelőző hónap után helyezték el, kivéve a 19. évet, (a ciklus utolsó évét) mikor az őszpontot tartalmazó hónap után illesztették be. Ez a rendszer az iszlám hódításokig (i.sz.VII.század) állt fenn.

Az Új Évet (akítu) a tavaszi napéjegyenlőség idején ünnepelték.

Ez a tény a körrel együtt még jobban kihangsúlyozza a Kos csillagkép 0. fokát, mint kiindulópontot az időben és a térben egyaránt.

A hónapoknak különböző neve volt, az egyes dinasztiák alatt, különféle városokban más-más elnevezéssel illették őket, előfordul, hogy egy hónap neve egy másik városban egy másik hónapot jelölt.

A sumér reneszánsz alatt a nippuri kalendáriumban a következő hónapnevek voltak:

1. hónap - Bára-zá-gar
2. hónap - Gud-si-su
3. hónap Sig-ga
4. hónap - Šu-numun
5. hónap - Ne-izi-gar
6. hónap - Kíg-Inanna (A betakarítás(Inanna, mint termékenység istennő) feladata
7. hónap - Du-kù
8. hónap - Apin-dug-a (szántás hónapja)
9. hónap - Gan-gan-é
10. hónap - Ab-ba-é
11. hónap - Zíz-a
12. hónap - Še-sag-ku (Lagasban 11. Urban 1. hónap, Ummában 1.hónap, Drehemben 12. Su-sin előtt, Su-sin után az 1. hónap)

A holdhónap 15. napjának Sabbatu volt a neve. A holdhónap utolsó napjának neve Bubbulu.

Az órákra való osztás a sumér számolási módszerre nyúlik vissza. Ők a tízes számrendszer mellett a nagyobb egységek jelölésére a hatvanas számrendszert alkalmazták. A napot, csakúgy mint a kört, 360 részre osztották. A napot és az éjszakát egyaránt 6-6 órára osztották, így kettős órákkal számoltak. Ez a módszer nagyjából megfelelt az akkori legpontosabb időmérő eszközöknek, a napóráknak. Ismerték és használták a homokórát is.

Sumér óra sematikusan, a napkelte pillanata:

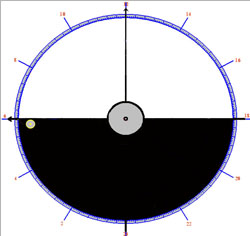
Current LuniSolar Model

The current explanation for why we see this precession of the equinox is that the tug of the Sun and the Moon acting upon the Earth’s bulge (<1% wider at equator) causes the Earth to gyrate so that the pole axis slowly traces a circle in the sky over about 24,000 to 26,000 years. This model, commonly seen in textbooks, mixes nutation with precession and obfuscates the fact that these are two separate phenomenons, one local and short in duration (nutation) and one non-local and very long in duration (precession).

The Lunisolor Precession theory was originally developed before there was any formal knowledge of binary stars or their motions, and before there was any recognition that the solar system might be moving. While this theory is a good first attempt at explaining the observed phenomenon (within a static solar system), it relies on certain untested assumptions concerning the composition and stability of the earth’s core and the moon’s solidity, and has had to be modified a number of times over the years to get the calculation to fit the ever changing observable. Most astronomers do not pay attention to precession theory and consider these changes to be minor tweaks but they are actually telltale signs of the problems with current theory.

Another problem with current theory is the moon is thought to be the principal force acting upon the oblate earth. However, the moon is slowly receding from the earth (thereby theoretically producing less torque) whereas the precession rate is slowly speeding up (an indication of a greater force at work). Few are aware of the changing rate of precession thus little attention has been paid to the fact that the observable seems to contradict the theory concerning the forces at work. To date, this issue has not been addressed in the literature. (Update: Since we began our work the IAU has come out with resolution P03, which notes that the current lunisolar precession theory “is not consistent with dynamical theory”. We are hopeful this will lead to an acknowledgement that the precession observable includes motion of the solar system relative to the VLBI reference points – and that this recognition will advance the eventual adoption of a precession model that accounts for more than just local dynamics).

And of course the biggest failure of the current lunisolar theory is it makes no allowance for the different reference frames (a moving solar system versus fixed stars) and therefore requires that the earth change orientation relative to all objects, near and far, at the same rate. Such is not the case.